Bryson-Denham Problem
The Bryson-Denham state-constrained double integrator problem optimal control problem is stated as follows. Minimize the cost functional $$ J = \textstyle{\frac{1}{2}}\displaystyle\int_0^1 u^2(t) dt$$ subject to the dynamic constraints $$\begin{array}{lcl}\dot{x}(t) & = & v(t), \\ \dot{v}(t) & = & u(t), \end{array}$$ and the boundary conditions $$\begin{array}{lclcl} x(0) & = & x(1) & = & 0, \\ v(0) & = & -v(1) & = & 1, \end{array}$$ and the state inequality path constraint $$x(t)\leq\ell.$$ The solution to the Bryson-Denham state-constrained double integrator problem using GPOPS-II is shown in the figures below for \(\ell=1/9\).
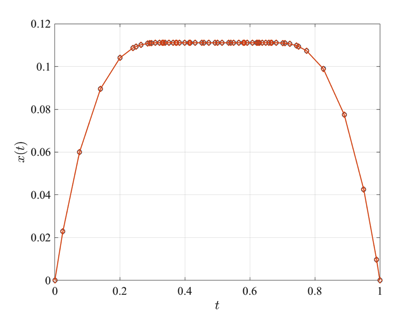

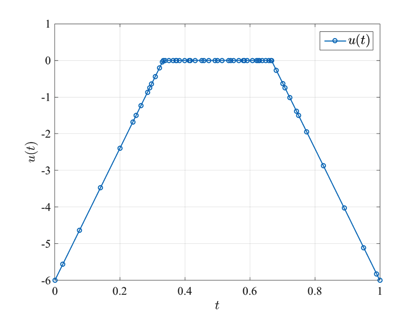
Image Courtesy of NASA. Photo ID: EC99-45145-2.

