Free Flying Robot
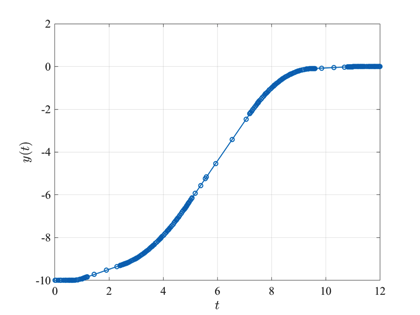
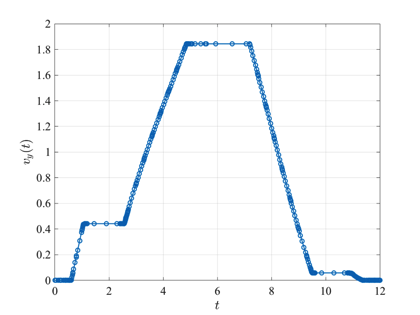
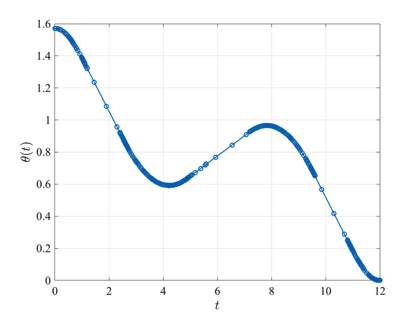
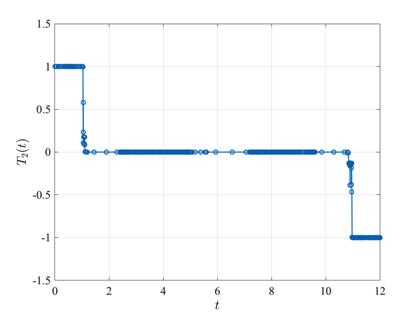
The free flying robot optimal control problem is stated as follows. Minimize $$J=\int_0^{t_f} (u_1(t)+u_2(t)+u_3(t)+u_4(t)) dt$$ subject to the dynamic constraints $$\begin{array}{lcl}\dot{x}(t) & = & v_x(t), \\ \dot{y}(t) & = & v_y(t), \\ \dot{v}_x(t) & = & (T_1(t)+T_2(t))\cos\theta(t), \\ \dot{v}_y(t) & = & (T_1(t)+T_2(t))\sin\theta(t), \\ \dot{\theta}(t) & = & \omega(t), \\ \dot{\omega}(t) & = & \alpha T_1(t) + \beta T_2(t), \end{array}$$ the boundary conditions $$\begin{array}{lcrclcr} x(0) & = & -10 & , & x(t_f) & = & 0, \\ y(0) & = & -10 & , & y(t_f) & = & 0, \\ v_x(0) & = & 0 & , & v_x(t_f) & = & 0, \\ v_y(0) & = & 0 & , & v_y(t_f) & = & 0, \\ \theta(0) & = & \pi/2 & , & \theta(t_f) & = & 0, \\ \omega(0) & = & 0 & , & \omega(t_f) & = & 0,\end{array}$$ and the control inequality path constraints $$ \begin{array}{cr} 0 \leq u_i(t) \leq 1000, & \quad (i=1,2,3,4),\\ T_i(t) \leq 1, & (i=1,2),\end{array}$$ where $$\begin{array}{lcrclcl} T_1(t) & = & u_1(t) - u_2(t) & , & T_2(t) & = & u_3(t) - u_4(t), \\ \alpha & = & 0.2 &, & \beta & = & 0.2. \end{array}$$