Hyper-Sensitive Problem
The hyper-sensitive optimal control problem is stated as follows. Minimize the cost functional $$J={\textstyle\frac{1}{2}}\displaystyle\int_0^{t_f}(x^2(t)+u^2(t))dt$$ subject to the dynamic constraint $$\dot{x}(t)=-x^3(t)+u(t)$$ and the boundary conditions $$\begin{array}{lcl}x(0) & = & 1.5, \\ x(t_f) & = & 1,\\ t_f & = & \textrm{Fixed}.\end{array}$$ The solution to the hyper-sensitive optimal control problem with \(t_f=10000\) using GPOPS-II is shown in the figures below.
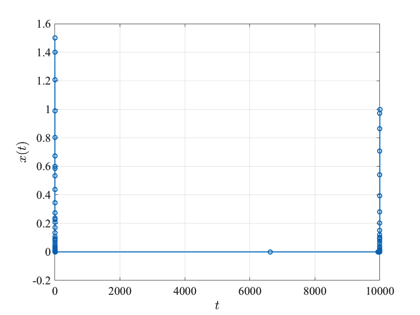
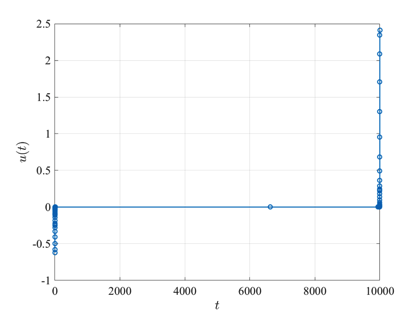
Image Courtesy of the United States Navy. URL. http://www.navy.mil/view_single.asp?id=3349. Used with Permission.

