Launch Vehicle Ascent Problem
The multiple-stage launch vehicle ascent optimal control problem is stated as follows. Minimize the cost functional $$J=-m(t_f)$$ subject in each phase to the dynamic constraints $$\begin{array}{lcl}\dot{\mathbf{r}}(t) & = & \mathbf{v}(t), \\ \dot{\mathbf{v}}(t) & = & \displaystyle\frac{T\mathbf{u}+\mathbf{D}}{m} + \mathbf{g}, \\ \dot{m}(t) & = & \displaystyle -\frac{T}{g_0 I_{sp}}, \end{array}$$ the control equality path constraint $$\|\mathbf{u}(t)\|_2=1$$ the phase continuity constraints $$\begin{array}{lcl}\mathbf{r}(t_f^{(i)}) & = & \mathbf{r}(t_0^{(i+1)}), \\ \mathbf{v}(t_f^{(i)}) & = & \mathbf{v}(t_0^{(i+1)}),\\ m(t_f^{(i)}) & = & m(t_0^{(i+1)}),\end{array}\quad (i=1,2,3),$$ the initial conditions $$\begin{array}{lcl}\mathbf{r}(0) & = & \mathbf{r}_0, \\ \mathbf{v}(0) & = & \mathbf{v}_0,\end{array}$$ and the terminal constraints $$\begin{array}{lcl}a(t_f) & = & a_f, \\ e(t_f) & = & e_f, \\ i(t_f) & = & i_f, \\ \Omega(t_f) & = & \Omega_f , \\ \omega(t_f) & = & \omega_f. \end{array}$$ The solution to the multiple-stage launch vehicle ascent problem obtained using GPOPS-II with the NLP solver SNOPT is shown in the figures below.
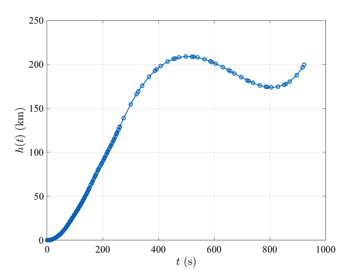


Image Courtesy of NASA.

