Orbit-Raising Problem
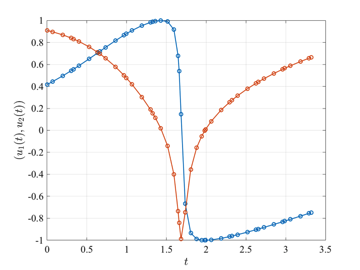
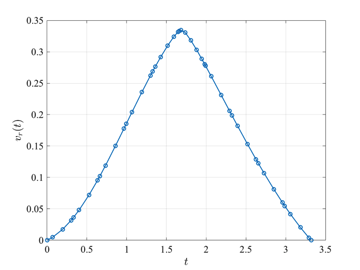
The orbit-raising optimal control problem is stated as follows. Maximize the cost functional $$J=r(t_f)$$ subject to the dynamic constraints $$\begin{array}{lcl} \dot{r} & = & v_r, \\ \dot{\theta} & = & \displaystyle \frac{v_\theta}{r}, \\ \dot{v}_r & = & \displaystyle \frac{v_\theta^2}{r} - \frac{\mu}{r^2} + a u_1, \\ \dot{v}_\theta & = & \displaystyle -\frac{v_r v_\theta}{r} + a u_2, \end{array}$$ the control equality path constraint $$u_1^2 + u_2^2 = 1,$$ and the boundary conditions $$\begin{array}{lclclcl} r(0) & = & 1 & , & r(t_f) & = & \textrm{Free}, \\ \theta(0) & = & 0 & , & \theta(t_f) & = & \textrm{Free}, \\ v_r(0) & = & 0 & , & v_r(t_f) & = & 0, \\ v_\theta(0) & = & 1 & , & v_\theta(t_f) & = & \displaystyle \sqrt{\frac{\mu}{r(t_f)}},\end{array}$$ where $$\begin{array}{lcl}a&=&\displaystyle \frac{T}{m_0 + \dot{m}t}, \\ m_0 & = & 1, \\ \dot{m} & = & -0.0749.\end{array}$$ The solution to the orbit-raising optimal control problem using GPOPS-II with the NLP solver IPOPT is shown in the figures below.