Reusable Launch Vehicle Entry Problem
The reusable launch vehicle optimal control problem is stated as follows. Maximize the cost functional $$J=\phi(t_f)$$ subject to the dynamic constraints $$\begin{array}{lcl} \dot{r} & = & v\sin\gamma, \\ \dot{\theta} & = & \displaystyle \frac{v\cos\gamma\sin\psi}{r\cos\phi}, \\ \dot{\phi} & = & \displaystyle \frac{v\cos\gamma\cos\psi}{r}, \\ \dot{v} & = & \displaystyle -\frac{D}{m} - g\sin\gamma, \\ \dot{\gamma} & = & \displaystyle \frac{L\cos\sigma}{m v} - \left(\frac{g}{v}-\frac{v}{r}\right)\cos\gamma, \\ \dot{\psi} & = &\displaystyle \frac{L\sin\sigma}{mv\cos\gamma} + \frac{v\cos\gamma\sin\psi\tan\phi}{r}, \end{array}$$ and the boundary conditions $$\begin{array}{lclclcl} h(0) & = & 79.248~\textrm{km} & , & h(t_f) & = & 24.384~\textrm{km}, \\ \theta(0) & = & 0~\textrm{deg} & , & \theta(t_f) & = & \textrm{Free}, \\ \phi(0) & = & 0~\textrm{deg} & , & \phi(t_f) & = & \textrm{Free}, \\ v(0) & = & 7.803~\textrm{km}\cdot\textrm{s}^{-1}, & , & v(t_f) & = & 0.762~\textrm{km}\cdot\textrm{s}^{-1}, \\ \gamma(0) & = & -1~\textrm{deg} & , & \gamma(t_f) & = & -5~\textrm{deg}, \\ \psi(0) & = & -90~\textrm{deg} & , & \psi(t_f) & = & \textrm{Free}. \end{array}$$ The solution to the hyper-sensitive optimal control problem with tf=10000 using GPOPS-II is shown in the figures below.
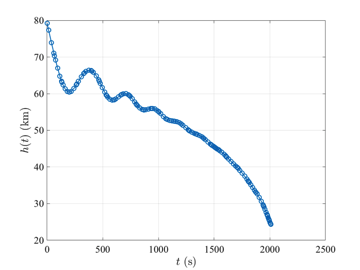
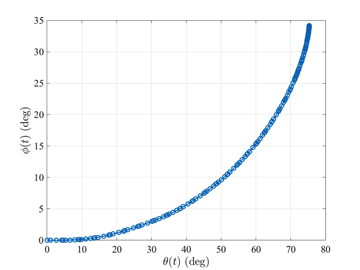

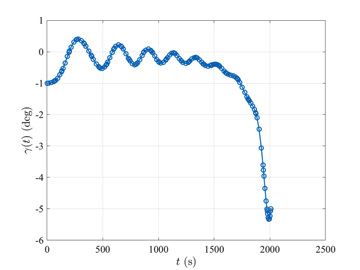

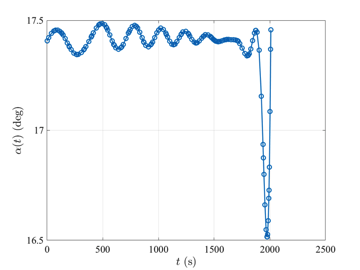

Image Courtesy of NASA.

