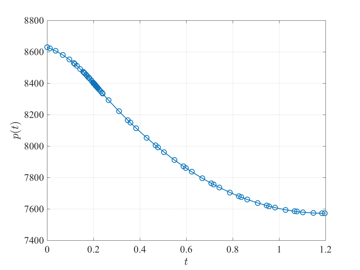
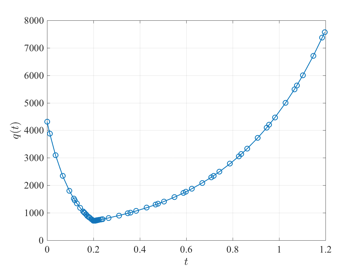
Tumor Anti-Angiogenesis Problem
The tumor anti-angiogenesis optimal control problem is stated as follows. Minimize the cost functional $$J=p(t_f)$$ subject to the dynamic constraints $$\begin{array}{lcl} \dot{p} & = & -\zeta p \log(p/q), \\ \dot{q} & = & q(b-\mu-d p^{2/3} + Gu),\end{array}$$ the boundary conditions $$\begin{array}{lcl} p(0) & = & p_0, \\ q(0) & = & q_0 \end{array}$$ the integral constraint $$\int_0^{t_f} u(t)dt\leq A, $$ and the control inequality path constraint $$0 \leq u(t) \leq u_{\max}.$$ The solution to the tumor anti-angiogenesis optimal control problem using GPOPS-II is shown in the figures below.